Eletricidade Básica – parte 2

1.2.4 - ELETROMAGNETISMO

Em 1819, um físico dinamarquês HANS CRISTIAN OERSTED aproximou uma pequena bússola de um fio, pelo qual passou uma corrente elétrica. Notou com isto que a agulha se movia. Quando desligou a corrente a agulha voltou-se para a posição normal. Esta descoberta desencadeou uma série de acontecimentos que contribuíram para dar forma a nossa civilização industrial.

A importância dessa descoberta estava no fato de que ficou provado que um condutor quando percorrido por uma corrente elétrica criava um campo magnético semelhante ao imã.

Supõe-se então que o movimento de uma partícula carregada seja sempre acompanhada por um campo magnético.

 

Fig. 7 - Campo magnético está estabelecido ao redor de um condutor pelo qual passa corrente.

1.3 - OS MULTIPLOS E SUBMULTIPLOS / NOTAÇÃO CIENTÍFICA

A fim de facilitar a compreensão de grandezas foram criados os múltiplos e submúltiplos de uma unidade padrão. Exemplos:

a - Um pacote de feijão tem 1000 gramas. Porém é mais fácil dizer 1 Quilograma (Kg), que é um múltiplo do grama.

b - Uma régua tem 0,3 metros. Dizendo que ela tem 30 centímetros (cm), entendemos mais fácil. O cm é um submúltiplo do metro.

Em negrito estão as notações científicas mais usadas

------------------------------

Regras matemáticas:

10^x x 10^y = 10^{x+ y}

10^x / 10^y = 10^x x 10^{- y}= 10^x-y

Só podemos somar quando temos o mesmo expoente: 10. 10^x + 5. 10^x = 15. 10^x

Vamos recordar:

Potência de 10: Na eletrônica e elétrica é normal usarmos potência de 10 para representar grandezas muito grandes ou pequenas:

----------------------------------------------------------------------------------------------------

Exercícios:

1) Escreva sob a forma numérica os valores em múltiplos e submultiplos do volt;

a) 1x10⁰ V = i) 100µV =

b) 10x10⁰ V = j) 100MV =

c) 100mV = l) 350KV =

d) 1V = m) 0,1mV =

e) 10KV = n) 0,1KV =

f) 10x10³ V = o) 550µV =

g) 10µV = p) 435mV =

h) 100x10^-6 V = q) 25x10 ^-3 V =

2) Escreva sob a forma de múltiplos e submultiplos, utilizando os símbolos, os valores numéricos da grandeza volt a seguir respeitando a notação científica.

a) 1000000 V = g) 0,000015V =

b) 0,001 V = h) 0,2135 V =

c) 0,0001 V = i) 39000 V =

d) 1000 V = j) 60000 V =

e) 1700 V = l) 18000000 V =

f) 0,000000015 V = m) 0,01 V =

-------------------------------------------------------------------

1.4 - GRÁFICOS:

1.4.1 – INTRODUÇÃO:

A razão do uso dos gráficos na área técnica está na rapidez e facilidade com que ele permite visualizar a modificação de um fenômeno. Nos hospitais, por exemplo, a variação de temperatura (febre) de um paciente costuma ser indicada por um gráfico. Nas indústrias a produção, venda, estoque, etc., também podem ser mostrados por gráficos.

Existem fenômenos que não podem ser representados por fórmulas matemáticas de maneira prática e, é ai, então, que o gráfico mostra sua real utilidade.

1.4.2 – CONCEITO :

Entende-se por gráfico a figura geométrica que representa, uma igualdade ou equação matemática. Exemplo:

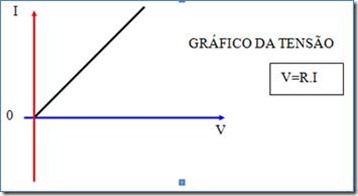
GRÁFICO DA TENSÃO

GRÁFICO DE POTÊNCIA

GRÁFICO CLÍNICO DE TEMPERATURA

Obs.: A temperatura de uma pessoa não obedece a qualquer equação matemática, mas é comum ser posta sob a forma de gráfico.

Observa-se que o gráfico mostra a variação de uma grandeza, em função de outra.

1.4.3 - Elementos do Gráfico:

1.4.3.1 - Eixos:

Nota-se nas figuras apresentadas que o gráfico tem dois segmentos de reta que se cortam, fazendo um ângulo de 90^o, esses segmentos denominam-se eixos. O eixo horizontal é chamado de eixo das abcissas e o eixo vertical, de eixo das ordenadas. Na prática, é comum nomear o eixo de acordo com a grandeza que ele representa.

1.4.3.2 - Graduação dos eixos:

Para que o gráfico seja útil precisamos marcar sobre seus eixos valores numéricos. Uma régua comum simboliza um eixo graduado, pois representa um segmento de reta, graduado em milímetros e numerado em centímetros. Exemplo de gráfico graduado:

1.4.3.3 - Coordenadas:

Os dois eixos do gráfico abaixo foram convenientemente graduados. Qualquer ponto da curva (ou reta) fica individualizado pela sua distância ao eixo horizontal e ao eixo vertical. A esse par de valores damos o nome de coordenadas.

O ponto que chamamos de P₁, tem coordenadas 0,7V e 2mA, o ponto P₂ tem coordenadas 1V e 1 mA.

Obs.: Os dois semi-eixos do gráfico podem ser prolongados, para a esquerda e para baixo, delimitando novas regiões. As graduações acima do eixo e à direita da origem são positivas, abaixo e à esquerda, são negativas.

Exemplo:

1.4.3.4 - Escala:

O eixo horizontal da figura 4 está graduado, entretanto cada segmento unitário tanto pode representar l Volt, como 100 Volts, 1 milivolt, etc. O mesmo acontece com o eixo vertical.

Ao se fixar o valor da grandeza que cada um dos segmentos unitários representa, estamos definindo a escala do gráfico.

A fim de facilitar a compreensão de grandezas foram criados os múltiplos e submúltiplos de uma unidade padrão. Como já foi visto em potência de 10. Exemplos :

a - Um pacote de feijão tem 1000 gramas. Porém é mais fácil dizer 1 Quilograma (Kg), que é um múltiplo do grama.

b - Uma régua tem 0,3 metros. Dizendo que ela tem 30 centímetros (cm), entendemos mais fácil. O cm é um submúltiplo do metro.